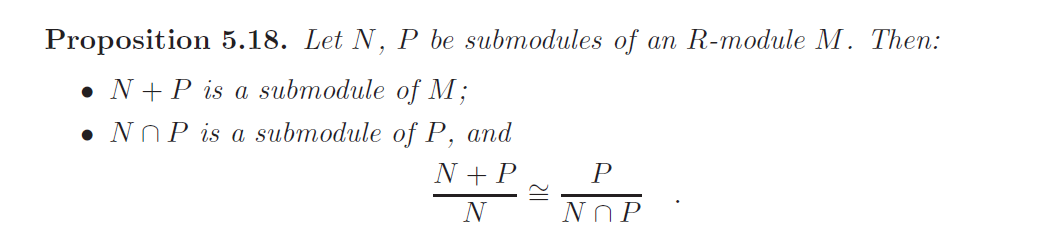环上的模
我们知道,对于一个群$G$,和$G$的正规子群$H$,我们可以作商群$G/H$,且两个群直接的同态的image 和kernel都是正规子群。而对于交换群,性质会更好:交换群$G$的任意子群$H$,我们都可以作商群$G/H$。然而,对于环来说,我们不能对一个环$R$的子环作商环,并且环同态的image和kernel都不是子环。环中重要的子集是理想,我们可以对环$R$的理想$I$作商环$R/I$,但是理想并不是环的子结构。所以环范畴的性质不如交换群范畴好,我们需要在环上引入一种更好的代数结构:模。
定义
简单来说,(左$R$)模是环$R$在交换群$M$的上的作用。即环同态
它可以诱导出作用$\rho$
记像$\rho(r,m)=rm$,该作用满足对于任意$r,s\in R,m,n\in M$
- $(r+s)m=rm+sm$
- $r(m+n)=rm+rn$
- $(rs)m=r(sm)$
- $1m=m$
反过来,满足上述三条性质的作用$\rho$,唯一确定了一个环同态$\sigma$,
称这个作用为左R-模。同样地,我们可以定义右R模。
简单性质与例子
$M$是左R-模,则
- $0m=0$
- $(-1)m=-m$
命题 交换群$G$是$\mathbb{Z}$-模,且该模是唯一的
证 :因为$\mathbb{Z}$是Ring范畴的initial object,故存在唯一的环同态
由于$\mathbb{Z}$-模也是交换群,故Z-Mod范畴与Ab范畴是等价的(等价这个词是否准确?)
R-Mod 范畴
(左)R-模之间的同态定义为保持模结构的群同态,设$M,M’$是R-模,则模同态$\varphi$满足,对任意$r\in R,m,m’\in M$
- $\varphi(m+m’)=\varphi(m)+\varphi(m’)$
$\varphi(rm)=r\varphi(m)$
显然,模同态的复合还是模同态,恒等映射是模同态,故所有R-模构成范畴R-Mod.
对于交换群范畴Ab来说,若$M,N\in \text{Obj(Ab)}$,则$\text{Hom}_{Ab}(M,N)\in \text{Obj}(Ab)$(如果再两个同态之间定义了加法,$M,N$的所有同态按加法构成交换群)
这个性质在R-Mod范畴中也成立。
若 $M,N\in \text{Obj(R-Mod)}$ , $\varphi\in \text{Hom}{\text{R-Mod}}(M,N)$ ,定义 $R$ 在 $\text{Hom}{\text{R-Mod}}(M,N)$ 上的作用则$\text{Hom}_{\text{R-Mod}}(M,N)$也是R-模
R-代数
任意环同态$\alpha :R\to S$可以诱导出R-模$S$:定义$R$在$S$(环$S$当然是交换群)上的作用
可以验证,在该作用下,$S$是R-模。若$R=S$,$\alpha=\mathrm{id}_R$,则$R$可以看出自身上的模。
若$R$是交换环,且$\alpha(R)$包含在$S$中心,即$\alpha(r)$与$S$的每个元素和换,则有
$R$的元素可以在$S$的乘法中自由移动,这时称$S$(或$\alpha$)为R-代数,若$S$还是除环,称$S$为R-可除代数,若$R$还是域,可简称可除代数。
R-Alg 范畴
R-代数之间的同态定义为保持模结构的环同态。若$\varphi$是R-代数$S$与$S’$的同态,则$\varphi$满足
足,对任意$r\in R,s,s’\in S$
- $\varphi(s+s’)=\varphi(s)+\varphi(s’)$
- $\varphi(ss’)=\varphi(s)\varphi(s’)$
- $\varphi(1)=1$
- $\varphi(rs)=r\varphi(s)$
显然,R-代数同态的复合还是R-代数同态,恒等映射是R-代数同态,故所有R-代数构成R-Alg范畴。
例子 $\mathbb{Z}$ -Alg 范畴
设$S$是$\mathbb{Z}$-代数,环同态
是被唯一确定的,且$ns=\underbrace{s+s+\cdots+s}_{n \ \text{time}}$
,故每一个环$S$都对于唯一的$\mathbb{Z}$-代数,而$\mathbb{Z}$-代数都是环,所以环与$\mathbb{Z}$-代数一一对应,Ring范畴与 $\mathbb{Z}$ -Alg 范畴可以看成是相同的。
子模与商
子模
R-模$M$的子集$N$称为是$M$的子模,如果$N$是R-模,且inclusion map $N\to M$是模同态
例子
环$R$看成自身上的R模,它的子模就是是$R$的理想(如果是左模就是左理想)
模同态$M\to M’$的image和kernel分别是$M’$和$M$的子模
商模
设$M$是左R-模,$N$是$M$的子模,则$N$是$M$的子群,我们可以作出商群$M/N$,自然映射$\pi:M\to M/N$是群同态,要使它为模同态,必须
即
所以,我们只需用上式定义$R$在交换群$M/N$上的作用(可以验证上式定义良好),就能使$M/N$成为R-模,且$\varphi$是模同态,称$M/N$为模$M$对$N$的商模
模同构定理
泛性质
设$M$是R-模,$N$是$M$的子模,对于任意模同态 $\varphi : M\to M’$满足$\text{ker}\varphi\supe N$,存在唯一的模同态$\tilde{\varphi}:M/N\to M’$使得$\tilde{\varphi} \circ \pi=\varphi$
映射分解定理

第一同构定理
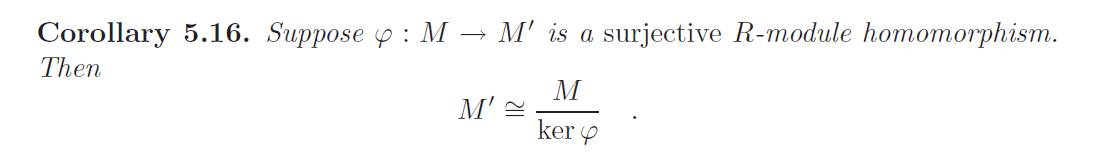
第三同构定理
$M/N$的子模与包含$N$的$M$的子模一一对应
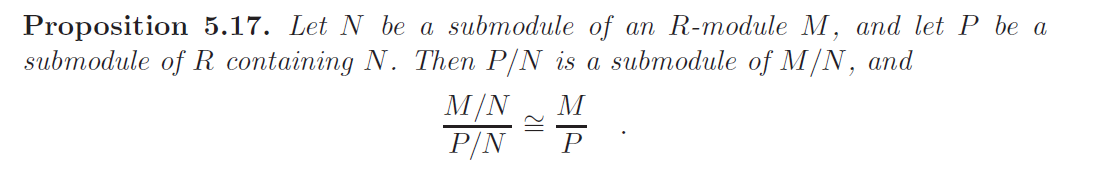
第二同构定理